最小生成树
定义:
加权图:加权图是图中每条边都关联一个权值的图模型(边的权重可以表示距离、时间、费用等不同变量;权中可正可负)
带权重边的表示:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35public class Edge implements Comparable<Edge> {
private int v;
private int w;//v,w为边连接的两个顶点
private double weight;//边的权重
public Edge(int v,int w,double weight){
this.v=v;
this.w=w;
this.weight=weight;
}
public double weight(){
return weight;
}
public int either(){
return v;
}
public int other(int vertex){
if(vertex==v){
return w;
}else if(vertex==w){
return v;
}else{
throw new RuntimeException("Inconsistent edge");
}
}
public int compareTo(Edge that){
if(this.weight()<that.weight()){
return -1;
}else if(this.weight()>that.weight()){
return 1;
}else{
return 0;
}
}
}
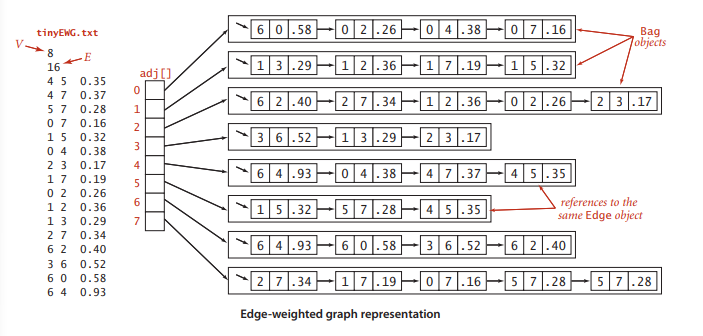
无向加权图的表示:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
public class EdgeWeightGraph {
private int V;
private int E;
private Bag<Edge>[] adj;
public EdgeWeightGraph(int V){
this.V=V;
this.E=0;
adj=(Bag<Edge>[])new Bag[V];
for(int v=0;v<V;v++){
adj[v]=new Bag<Edge>();
}
}
public int V(){
return V;
}
public int E(){
return E;
}
//添加边
public void addEdge(Edge e){
int v=e.either();
int w=e.other(v);
adj[v].add(e);
adj[w].add(e);
E++;
}
public Iterable<Edge> adj(int v){
return adj[v];
}
//返回图中所有的边
public Iterable<Edge> edges(){
Bag bag=new Bag<Edge>();
for(int v=0;v<V;v++){
for(Edge e:adj[v]){
if(e.other(v)>v){
bag.add(e);
}
}
}
return bag;
}
//显示图表
public String toString(){
StringBuilder s=new StringBuilder();
s.append(V+"Vertexs"+E+"Edges\n");
for(int v=0;v<V;v++){
s.append(v+":");
for(Edge e:adj[v]){
s.append(e+" ");
}
s.append("\n");
}
return s.toString();
}
} 
生成树:一幅图的生成树是它的一棵含有其所有顶点的无环连通子图
最小生成树(MST):一幅图的最小生成树是它的一棵所有边权值和最小的生成树(生成树+所有边权值和最小)
切分定理
图的切分:将图中所有的顶点分为两个非空且不重叠的两个集合,横切边(crossing edge)是一条连接两个属于不同集合中顶点的边
切分定理:一幅加权图中,对于图的任意切分的横切边中的权重最小的边一定属于改图的最小生成树
切分定理会把加权图所有的顶点分为两个集合,检查每次切分的横切边并识别属于最小生成树的边
最小生成树的贪心算法: 生成最小生成树的基础是切分定理,对于一个V个顶点的加权图,使用切分定理找到最小生成树的一条边,不断重复直到找到最小生成树所有的V-1条边
最小生成树Prim算法
prim算法的核心是选取一个顶点,每一次向树中添加一条边,知道添加V-1条边;每次添加的边是连接树中的顶点和不在树中的顶点所连接的边中权重值最小的。
注:
连接树:最小生成树的一部分
横切边:为连接树中的顶点和不在连接树中的顶点之间的所有边
失效边:如果一条边的两个顶点都在连接树中,则为失效边不去管它
prim算法延时实现过程:
- 选取一个起始顶点作为生成树的第一个顶点,将此时所有的横切边加入优先队列(MinPQ)
- 检查队列
while(队列不空):
取出并删除队列中的权重值最小的边
if(这条边失效) contuine结束此次循环
if(这条边有一个顶点不在连接树上)将这个顶点添加到树中,并将新的横切边添加到优先队列中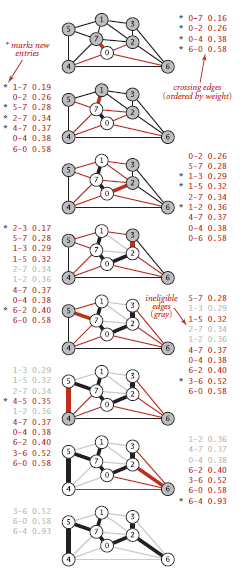
算法改进:prim算法即时实现
延时实现是一些失效的横切边保存在优先队列中(当向连接树添加一个新的顶点v时,所有和v相关联的横切边都会被加入到优先队列中),只有要删除的时候才检查它的有效性
Prim实时实现是不去保存所有的横切边,它只保存连接树顶点和非树顶点中权重最小的边
试想:当我们向连接树中添加了一个新的顶点v,那么非树顶点w可能距离连接树的距离更近了,我们只保存非树顶点w和树顶点距离最近的那条边。可能队列中保存着w到连接树的权重最小的边w->k,当连接树中加入了v之后,w->v这条边的权重值比w->k的权重值要小,那么在优先队列中对于顶点w,它和连接树距离最短的边更新为w->v。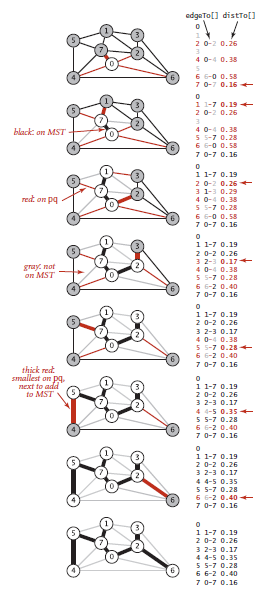
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55public class PrimMST{
private Edge[] edgeTo;//用来存储非树顶点距离树最近的边
private double[] distTo;//用来存储边的权重,distTo[i]=edgeTo[i].weight()
private boolean[] marked;//用来标记顶点是否在树中
private IndexMinPQ<Double> pq;//存储有效的横切边
public PrimMST(EdgeWeightGraph G){
edgeTo=new Edge[G.V()];
distTo=new double[G.V()];
marked=new boolean[G.V()];
pq=new IndexMinPQ<Double>(G.V());
for(int i=0;i<G.V();i++){
distTo[i]=Double.POSITIVE_INFINITY;
}
//从顶点0开始
distTo[0]=0.0;
pq.insert(0, 0.0);
while(!pq.isEmpty()){
visit(G,pq.deleteMin());
}
//当向最初的树中添加V-1条边后,最小生成树完成而优先队列变为空
}
private void visit(EdgeWeightGraph G,int v){
//将v添加至树中,更新相关数据
marked[v]=true;
//遍历和v相连的每一个顶点
for(Edge e:G.adj(v)){
int w=e.other(v);
if(marked[w]){
continue;
}
//检查distTo中存储的是否是w距树最小的距离
if(e.weight()<distTo[w]){
edgeTo[w]=e;
distTo[w]=e.weight();
//添加或更新优先队列中的相关顶点的数据
if(pq.contains(w)){
pq.changeKey(w, distTo[w]);
}else{
pq.insert(w, distTo[w]);
}
}
}
}
//遍历最小生成树中的所有边
public Iterable<Edge> edges(){
Queue<Edge> q=new Queue<Edge>();
for(int v=0;v<edgeTo.length;v++){
Edge e=edgeTo[v];
if(e!=null){
q.enqueue(e);
}
}
return q;
}
}
Kruskal算法
Kruskal算法的核心是将图中所有的边按权重由小到大的顺序加入最小生成树,新加入的边不能与已经加入的边构成环。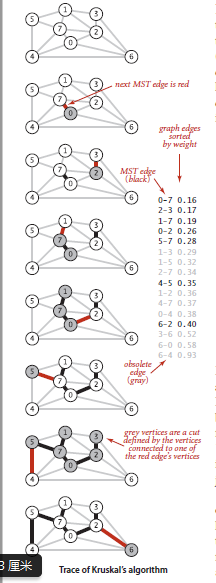
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public class KruskalMST {
private Queue<Edge>mst;
public KruskalMST(EdgeWeightGraph G){
mst=new Queue<Edge>();
//创建最小优先队列,并存储图中所有的边
MinPQ<Edge> pq=new MinPQ<Edge>(G.E());
for(Edge e:G.edges()){
pq.insert(e);
}
//创建并查集Union_Find中的一个形式Quick_find
Quick_find uf=new Quick_find(G.V());
while(!pq.isEmpty() && mst.size()<G.V()-1){
Edge e=pq.deleteMin();
int v=e.either();
int w=e.other(v);
//判断这条边的两个顶点是否连通,如果已经连通那么再加入这条边就会形成一个环
if(uf.connected(v, w)){
continue;
}
uf.union(v, w);
mst.enqueue(e);
}
}
public Iterable<Edge> edges(){
return mst;
}
}