Java算法-查找（散列表）

发表于 | 分类于

散列查找

在查找算法中如果利用数组将要存储的键作为数组索引下标，将对应的值作为数组的内容，在预先知道所要查找的内容在数组的下标可以实现快速查找，实现时间复杂度为O(1)的算法。由于键值可能是各种类型的，可能是整数、可能是字符串类型不能直接作为数组的索引，所以第一步就是要通过散列函数将键转化为数组的索引值。由于散列函数在转化过程中不同的键可能变成相同的索引值，出现碰撞冲突，所以第二步就要处理碰撞冲突。

散列函数

如果保存键值的数组大小为M，那么键值通过散列函数就要转化在[0,M-1]的索引范围内，我们需要的散列函数能够将键值均匀的分布在[0,M-1]内，每个键都有相同的可能与0~M-1红的每个整数对应。

我们所使用的散列函数能够均匀并独立的将所有的键分布于0到M-1之间

由于键值的数据类型不同，所需要的散列函数也不同，每种类型都有与之对应的散列函数

  1. 整数类型
    对于整数类型常用的方法是除留余数法:k%M
    最好使用不是2的幂的质数
  2. 浮点数
    将键表示为二进制然后使用除留余数法
  3. 字符串
    下面为String类型中计算hash值得算法 
1
2
3
4
5
6
7
8
9
10
11
public int hashCode() {
    int h = hash; //hash是初始值，一般为0
    if (h == 0 && value.length > 0) {
        char val[] = value;
        for (int i = 0; i < value.length; i++) {
            h = 31 * h + val[i];
        }
        hash = h;
    }
    return h;
}
  1. 组合键
    下面为自定义类的hashcode算法，它将类中的所有成员变量综合起来计算hash值

默认的hashcode函数返回对象的地址 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class Person {
	private String name;
	private int age;
	private String sex;
	private String city;
	public int hashCode() {
		final int prime = 31;
		int result = 1;
		result = prime * result + age;
		result = prime * result + ((city == null) ? 0 : city.hashCode());
		result = prime * result + ((name == null) ? 0 : name.hashCode());
		result = prime * result + ((sex == null) ? 0 : sex.hashCode());
		return result;
	}
}
  1. 将hashcode()的返回值转化为数组索引 
1
2
3
4
  
public int hash(Key k){
	return (k.hashCode() & 0x7fffffff) % M;
}

&的作用是将计算出的hashCode值得符号位屏蔽

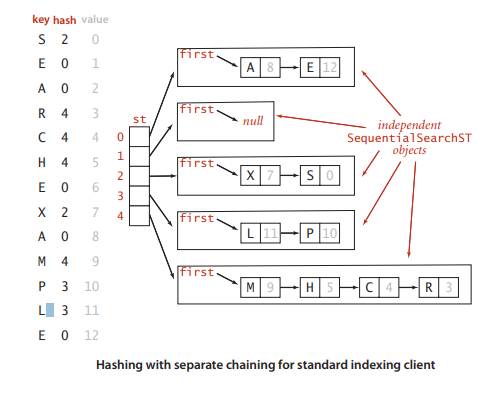
基于拉链法的散列表

拉链法：保存数组的大小为M，将数组的每一个元素指向一个链表，每个链表中都存储键值相同的元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
  
public class SeparateChainingHashST<Key,Value> {
	private int N;//键值对总数
	private int M;//散列表大小
	private SequentialSearchST<Key,Value>[] st;//存储链表的数组
	public SeparateChainingHashST(int M) {
		this.M = M;
		st=(SequentialSearchST<Key,Value>[]) new SequentialSearchST[M];
		for(int i=0;i<M;i++){
			st[i]=new SequentialSearchST();
		}
	}
	private int hash(Key key){
		return (key.hashCode() & 0x7fffffff) % M;
	}
	public Value get(Key key){
		return st[hash(key)].get(key);
	}
	public void put(Key key,Value val){
		st[hash(key)].put(key, val);
	}
	public void delete(Key key){
		st[hash(key)].delete(key);
	}
	public Iterable<Key> keys(){
		Queue<Key> queue=new Queue<Key>();
		for(int i=0;i<M;i++){
			for(Key key:st[i].keys()){
				queue.enqueue(key);
			}
		}
		return queue;
	}
}

拉链法的散列表性能分析：

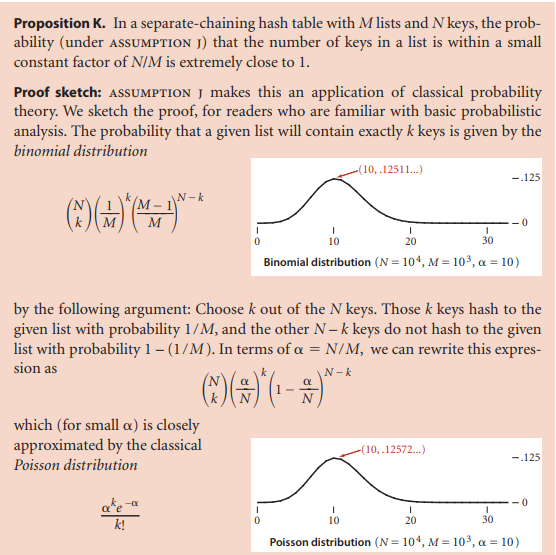
一张含有M个链表和N个键的散列表中，未命中的查找和插入所需要的比较次数大约为N/M

需要选择合适的M：如果M过大会空链表多浪费空间资源，但查找速度快；M过小链表平均长度变长，查找效率低；应该选择足够大的M能够将性能提高M倍。
也可以选择动态调整数组大小

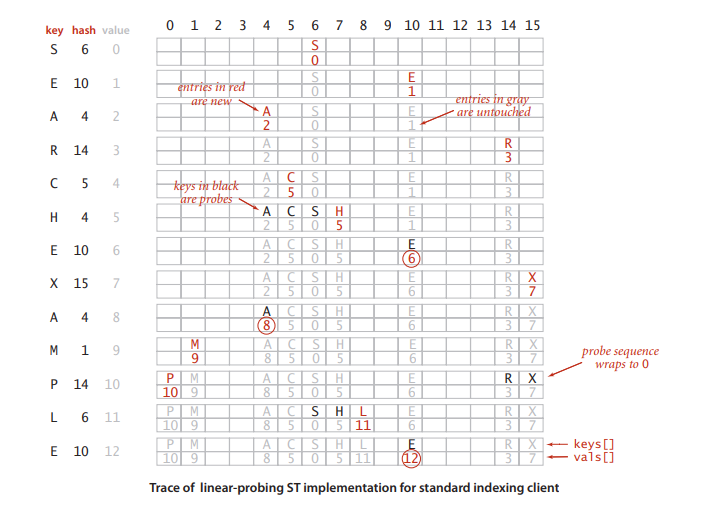
基于线性探测法的散列表（开放地址散列表）

线性探测法：通过哈希函数将键值k转化成数组索引值n，检查数组索引为n的位置会出现三种情况

  • 该位置键值为空，将键值对插入该位置
  • 该位置的键和被查找的键相同，如果查找操作返回查找内容，如果插入操作将键所对应的值换成新值
  • 该位置的键和被查找的键不同，则增大索引继续检查下一个键值，知道找到该键或者遇到一个空元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
public class LinearProbingHashST<Key,Value> {
	private int N;
	private int M;
	private Key[] keys;
	private Value[] vals;
	public LinearProbingHashST(int M){
		this.M=M;
		keys=(Key[]) new Object[M];
		vals=(Value[]) new Object[M];
	}
	private int hash(Key key){
		return (key.hashCode() & 0x7fffffff) % M;
	}
	public boolean contains(Key key){
		return get(key)!=null;
	}
	private void resize(int cap){
		LinearProbingHashST<Key,Value> t=new LinearProbingHashST<Key,Value>(cap);
		for(int i=0;i<M;i++){
			if(keys[i]!=null){
				t.put(keys[i], vals[i]);
			}
		}
		keys=t.keys;
		vals=t.vals;
		M=t.M;
	}
	public void put(Key key,Value val){
		//N/M>=1/2调整到1/4，使N/M保持在(1/8~1/2)
		if(N>=M/2){
			resize(2*M);
		}
		for(int i=hash(key);keys[i]!=null;i=(i+1)%M){
			if(key.equals(keys[i])){
				vals[i]=val;
				return;
			}
			keys[i]=key;
			vals[i]=val;
			N++;
		}
	}
	public Value get(Key key){
		for(int i=hash(key);keys[i]!=null;i=(i+1)%M){
			if(keys[i].equals(key)){
				return vals[i];
			}
		}
		return null;
	}
	public void delete(Key key){
		if(!contains(key)){
			return;
		}
		int i=hash(key);
		while(!keys[i].equals(key)){
			i=(i+1)%M;
		}
		keys[i]=null;
		vals[i]=null;
		i=(i+1)%M;
		while(keys[i]!=null){
			Key k=keys[i];
			Value v=vals[i];
			keys[i]=null;
			vals[i]=null;
			N--;
			put(k,v);
			i=(i+1)%M;
		}
		N--;
		if(N>0 && N<=M/8){
			resize(M/2);
		}	
	}
	public Iterable<Key> keys(){
		Queue<Key> queue=new Queue<Key>();
		for(int i=0;i<M;i++){
			if(keys[i]!=null){
				queue.enqueue(keys[i]);
			}
		}
		return queue;
	}	
}

线性探测法的性能分析：
开放地址类的散列表的性能依赖于散列表的使用率p=N/M，我们一般会动态调整数组的大小是p保持在1/8~1/2之间。

在一张大小为M并包含有N=pM个键的基于线性探测的散列表中，命中和非命中查找所需要的探测次数为：
~1/2(1+1/(1-p))和~1/2(1+1/(1-p)*(1-p))

当p趋近1时，查找次数趋近于无穷；当p=1/2时，查找次数在[1.5,2.5]的范围呃内；所以动态调整数组大小减小p避免连列表过满，散列表快满时所需要的查找次数非常大。

散列表能够使查找和插入操作在时间复杂度上为常数级，理论上是最优的性能.

但它也有几个问题:

  1. 散列函数 :每种数据类型都需要优秀的散列函数，散列函数的计算可能复杂昂贵，一个好的散列函数直接影响着散列表的性能。
  2. 散列表不支持有序性操作：散列表中的键是无序的，如果你想快速找到最大最小值或者某个范围的键，散列表不合适因为这些操作都是线性级别的。