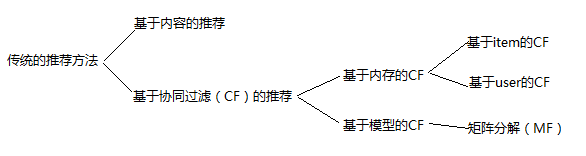
传统非深度学习的推荐方法主要分为两大类:基于内容的推荐和基于协同过滤的推荐。
一、 基于内容的推荐
基于内容的推荐主要思路是:根据用户过去喜欢的物品,为用户推荐和他过去喜欢的物品相似的物品。这个过程中最重要的是通过用户的历史行为来学习用户的偏好,刻画出用户画像,然后通过相似性度量找出与用户偏好最接近的 N 个物品。
基于内容推荐主要流程
- 物品表示(Item Representation):为每个 item 抽取出一些特征(也就是 item 的 content 了)来表示此 item。
- 用户偏好学习(Profile Learning):利用一个用户过去喜欢(及不喜欢)的 item 的特征数据,来学习出此用户的偏好特征(profile);
- 生成推荐列表(Recommendation Generation):通过比较上一步得到的用户 profile 与候选 item 的特征,为此用户推荐一组相关性最大的 item
基于内容的推荐,最重要的不是推荐算法,而是内容挖掘和分析。 内容挖掘和分析过程中,挖掘侧重于信息的探索和发现,分析侧重于信息的提炼和转化。在这里,内容分析往往是指关键词的提取,涉及非结构文本内容的结构化处理。如文本向量化处理。
用户画像由两个部分构成,一部分是对用户端内容挖掘分析后的用户的属性特征,另一部分是根据用户行为数据统计或学习到的对物品端结构化属性的偏好度量。
用户端的内容分析一般可以从人口统计学信息入手(如性别、年龄、婚姻状况、职业等),还可以对用户的个人签名、发表的评论、动态、日记等内容进行分析提炼关键特征。
基于内容推荐算法的优点
原理简单,易于实现,可以快速上线,且易于定位问题,常用于推荐系统起步阶段。
可解释性非常强,因为给用户推荐是和他过去喜欢的物品相似的物品。
用户之间具有独立性。这是与协同过滤截然不同的一点,基于内容的推荐算法都是依据他自身的历史数据来推荐的,自然就与他人的行为无关。而协同过滤算法刚好相反,它需要利用很多人的数据,基于内容的这种用户独立性也为推荐系统带来的一个显著好处,就是是别人不管对物品如何作弊(比如利用多个账号把某个产品的排名刷上去)都不会影响到自己。
- 物品没有冷启动问题,因为物品的内容特征不依赖于用户数据,新的物品可以立刻得到推荐,具有和老物品相同的曝光机会;同时推荐出的物品不会存在过于热门的问题。相对而言,基于协同过滤的新物品必须要有用户行为才能被推荐给其他用户。
基于内容推荐算法的缺点
物品的特征抽取一般很难。基于内容的推荐算法的前提是必须能够抽取出有意义的特征,且要求这些特征内容有良好的结构。这一步非常重要,因为特征质量决定了推荐系统性能的上界。
无法挖掘出用户的潜在兴趣,推荐精度较低。因为内容推荐只依赖于用户过去对某些物品的喜好,它产生的推荐也都会和用户过去喜欢的物品相似。如果一个人以前只看与推荐有关的文章,则只会给他推荐更多与推荐相关的文章,它不会知道用户可能还喜欢数码,推荐的都是相似物品,差异性不大,无法给用户带来惊喜感。
无法为新用户产生推荐,无法解决用户的冷启动问题,新用户没有喜好历史,自然无法获得他的偏好特征,所以也就无法为他产生推荐了。当然,这个问题协同过滤也有。
二、 基于协同过滤的推荐
协同过滤(Collaborative filtering,CF)是应用最广泛的推荐算法,在推荐领域占有极其重要的地位,甚至 “协同过滤” 一度成为推荐系统的代名词。
协同过滤的分类:协同过滤可以分为基于记忆(Memory-based)和基于模式(Model-based)两大类,其中基于记忆的协同过滤又可分为基于人口统计学(Demographic-based)和基于近邻(Neighborhood-based)两个子类,基于近邻又可分为基于用户(User-based)和基于物品(Item-based)两个小类.
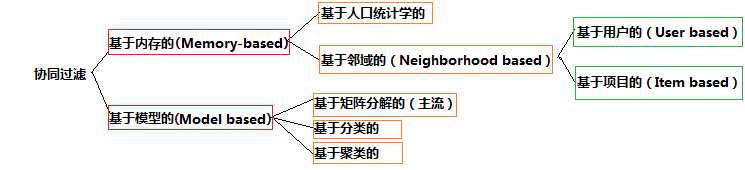
基于用户和基于物品的CF
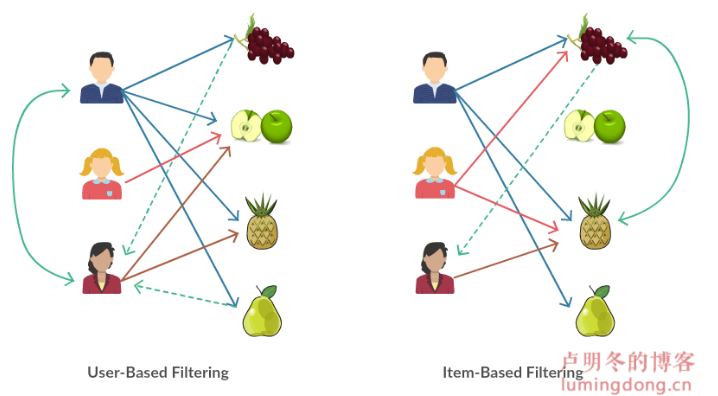
基于用户的协同过滤
1) 找到和目标用户兴趣相似的用户集合。
2) 找到这个集合中的用户喜欢的,且目标用户没有听说过的物品推荐给目标用户
基于物品的协同过滤
1) 计算物品之间的相似度。
2) 根据物品的相似度和用户的历史行为给用户生成推荐列表。
相似度计算公式
1 欧式距离
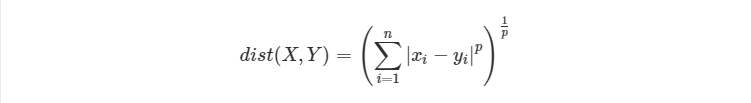
2 Jaccard 相似度
Jaccard 中文名为杰卡德系数、杰卡德相似度,公式为:
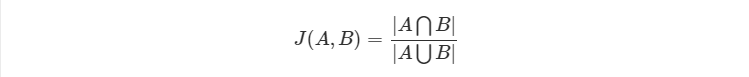
3 余弦相似度(Cosine Similarity)
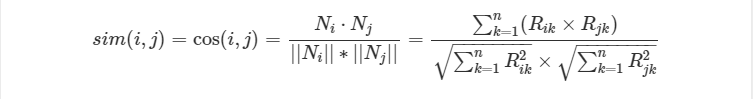
余弦相似度还有一种比较常见的形式,如下:

4 修正余弦相似度(Adjusted Cosine Similarity)
修正余弦相似度,是指中心化(减去平均值)后再求余弦相似度,计算公式如下:

- 为什么减去均值 ?
修正的余弦相似度和皮尔逊相似度都对向量进行了去均值操作,使用用户平均分对各独立评分进行修正,去掉用户在评分习惯上的差异性,减小了用户评分的偏置影响,这样可以使得双方都处于同一 “标准线”,中心位置都是 0,此时再进行相似度度量就会好很多了。当然 ,用户平均分也可以换成物品平均分,这样可以减少物品偏置对结果的影响。
5 皮尔逊相似度(Pearson Correlation Similarity)
皮尔逊相似度又常被称为皮尔逊相关度、皮尔逊相关系数,计算公式如下:

- 修正的余弦相似度与皮尔逊之间的区别?
皮尔逊系数的分母采用的评分集是两个用户的共同评分集(就是两个用户都对这个物品有评价),而修正余弦系数则采用两个用户各自的评分集。
UserCF和ItemCF的区别
基于用户的协同过滤和基于物品的协同过滤虽然很相似,但是在实际使用中,区别还是非常大的,下面总结了二者的主要区别,也是在实际应用中两种算法的择优选择依据。就目前工业界来看,使用 ItemCF 要比使用 UserCF 要多很多。
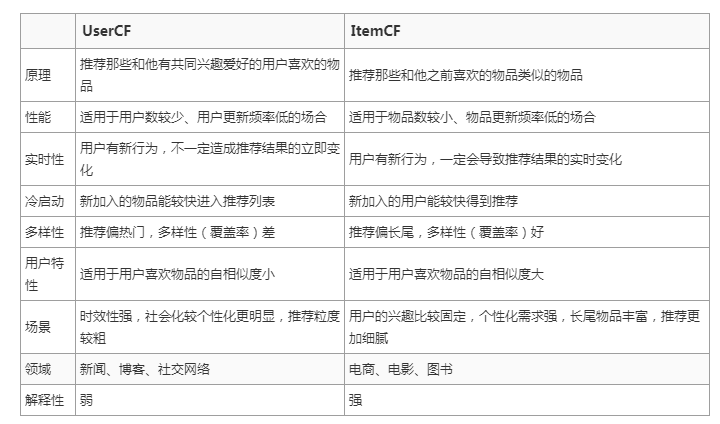
优缺点
协同过滤算法的优点
- 基于用户行为,因此对推荐内容无需先验知识
- 只需要用户和商品的关联矩阵即可,结构简单
- 在用户行为丰富的情况下,效果好
基于协同推荐算法的缺点
- 需要大量的显性/隐形的用户行为,有冷启动问题
- 假定用户的兴趣完全取决于之前的行为,没有考虑到当前的上下文环境
- 需要通过完全相同的商品关联,相似的不行
- 在数据稀疏的情况下易受影响,可以考虑二度关联。
三、矩阵分解
1. SVD
奇异值分解(SVD)在直接用于推荐的使用过程中存在很多问题:
- SVD 分解要求矩阵是稠密的,而现实场景中的评分矩阵是稀疏的,有大量空白,无法直接使用 SVD 分解的。要想使用 SVD,必须对评分矩阵中的缺失值进行简单的补全,比如用全局平均值或者用用户物品平均值补全,得到补全后的矩阵。接着可以用 SVD 分解并降维。但填充本身会造成很多问题,其一,填充大大增加了数据量,增加了算法复杂度。其二,简单粗暴的数据填充很容易造成数据失真。
- SVD 分解的复杂度比较高,假设对一个 m×n 的矩阵进行分解,时间复杂度为 O(n^2∗m+n∗m^2),其实就是 O(n^3)。对于 m、n 比较小的情况,还是勉强可以接受的,但是在推荐场景的海量数据下,m 和 n 的值通常会比较大,可能是百万级别上的数据,这个时候如果再进行 SVD 分解需要的计算代价就是很大的。
FunkSVD
既然将一个矩阵做 SVD 分解成 3 个矩阵很耗时,同时还面临稀疏的问题,那么我们能不能避开稀疏问题,同时只分解成两个矩阵呢?也就是说,现在期望我们的矩阵 R 这样进行分解:
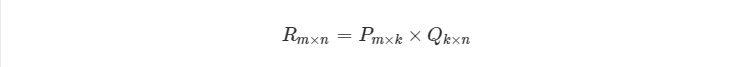
那么 FunkSVD 如何将稀疏的矩阵 R 分解成合理的 P 和 Q 呢?
这里便用到了到了机器学习算法,实际上是应用线性回归的思想,我们的目标是让用户已有评分和用矩阵乘积得到的评分残差尽可能的小,所以用均方差作为损失函数,来寻找最终的 P 和 Q。即通过 User-Item 评分信息来学习到的用户特征矩阵 P 和物品特征矩阵 Q,通过重构的低维矩阵预测用户对物品的评分。

有了目标函数,一般通过梯度下降法来进行优化得到最终结果。

BiasSVD
BiasSVD 是在 FunkSVD 的基础上加了偏置项特征。
偏置部分主要由三个子部分组成,分别是
- 训练集中所有评分记录的全局平均数 μ,表示了训练数据的总体评分情况,对于固定的数据集,它是一个常数。
- 用户偏置 bu,独立于物品特征的因素,表示某一特定用户的打分习惯。例如,对于批判性用户对于自己的评分比较苛刻,倾向于打低分;而乐观型用户则打分比较保守,总体打分要偏高。
- 物品偏置 bi,独立于用户兴趣的因素,表示某一特定物品得到的打分情况。以电影为例,好片获得的总体评分偏高,而烂片获得的评分普遍偏低,物品偏置捕获的就是这样的特征。
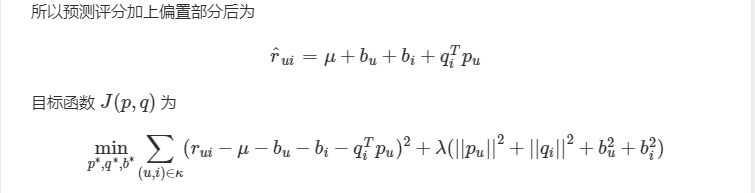
SVD++
SVD++是对 BiasSVD 的进一步改进,引入了隐式反馈和用户属性的信息,相当于引入了额外的信息源,这样可以从侧面反映用户的偏好,而且能够解决因显式评分行为较少导致的冷启动问题。
先说隐式反馈怎么加入,方法是:除了假设评分矩阵中的物品有一个隐因子向量外,用户有过行为的物品集合也都有一个隐因子向量,维度是一样的。把用户操作过的物品隐因子向量加起来,用来表达用户的兴趣偏好。
类似的,用户属性如社会学统计信息,全都转换成 0-1 型的特征后,对每一个特征也假设都存在一个同样维度的隐因子向量,一个用户的所有属性对应的隐因子向量相加,也代表了他的一些偏好。
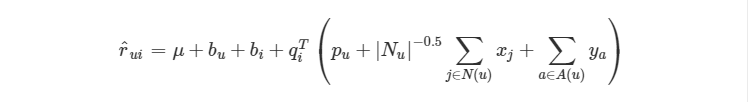
NMF
WRMF
之前的矩阵分解算法都是针对显式反馈的评分矩阵的,因此当数据集只有隐式反馈时,应用上述矩阵分解直接建模会存在问题。主要有两方面的原因,首先,隐式反馈数据集中只存在正样本,此时,不能够只使用正样本进行优化,而忽略了未观测样本。其次,不能够把所有的未观测样本都当做是负样本,因为这些未观测的样本既可能是用户不喜欢,也有可能是用户未曾看到但是实际上是喜欢的。One-Class 数据也是隐式反馈的通常特点。、
为了解决该问题,引入 WRMF (weighted regularized matrix factorization)。该方法对每个训练样本都加一个权重,来表征用户对物品偏好的置信度。这个权重通常使用隐式反馈行为的次数或者一些量化指标的转换,比如浏览次数或观看时间等。权重可以减少未知样本的影响力,这些未知样本的权重一般的比观测样本的权重小的多。
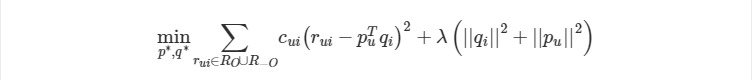
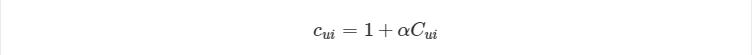
PMF
概率矩阵分解
BPR 贝叶斯个性化排序
推荐的整个流程可以分为召回、排序、重排序这三个阶段,通俗来说,召回就是找到用户可能喜欢的几百条资讯,排序就是对这几百条资讯利用机器学习的方法预估用户对每条资讯的偏好程度,一般以点击率衡量,也就是点击率预估问题。不难看出,排序学习在推荐领域主要用于排序阶段,最常用的是 Pointwise 排序方法;重排序更多是考虑业务逻辑的规则过滤,如在推荐结果的多样性、时效性、新颖性等方面进行控制。