决策树
决策树是一种常用的机器学习算法,该算法模型呈树形结构,在分类问题中,表示基于特征对实力进行分类的过程,以西瓜书中西瓜分类为例构建决策树对西瓜进行二分类。
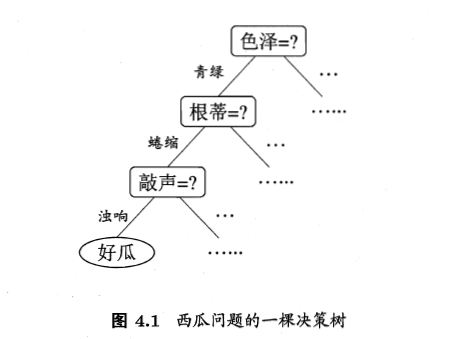
决策树的学习
给定数据集样本,构建一棵决策树能够对实力进行正确的分类。

决策树学习算法通常是一个递归地选择最优特征,根据特征对数据集进行分割,使得对各个子数据集有一个最好的分类的过程。
首先构建根节点,将所有训练数据放在根节点,选择一个最优的特征,按照这一特征将训练数据集分割成自己,使得各个自己有一个在当前条件下最好的分类。如果有子集已经被正确的分类,那么构建叶子结点,并将这些子集分到所对应的叶子结点中去;若还有子集没有被正确分类,那么对这些子集选择最优特征,继续进行分割,直到所有训练子集都被正确分类,或者没有合适的特征为止,生成了一棵决策树。(特征选择->决策树生成)
以上生成的决策树可能对训练数据有很好的的分类能力,但是对于新的测试样本未必有很好的分类能力,即发生过拟合现象。所以需要对已生成的树自下而上进行剪枝、使树变得简单,具有更好的泛化能力。(剪枝)
决策树学习算法主要包括三个过程:特征选择、决策树的生成和决策树的剪枝过程。1. 特征选择
特征选择在于选取对训练数据具有分类能力的特征,以提高决策树学习的效率。
通常特征选择的准则是信息增益或者信息增益比。1) 信息增益
熵(entropy)H(p) 是表示随机变量不确定性的度量,熵越大,随机变量的不确定性越大。当 p=0 或 p=1 时 H(p)=0, 随机变量玩却没有不确定性,而当p=0.5时,H(p)=1, 熵最大,随机变量的不确定性最大。
条件熵 (conditional entropy)H(Y|X) 表示在已知随机变量X的条件下随机变量Y的不确定性。随机变量X给定的条件下随机变量Y的条件熵定义为X给定条件下Y的条件概率分布的熵对X的数学期望:
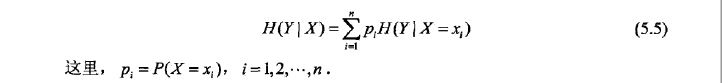
信息增益表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。


信息增益的特征选择方法:对于训练数据集/子集 D, 计算其每个特征的信息增益,并比较他们的大小,选择信息增益最大的特征。


2) 信息增益比
信息熵倾向于选择取值比较多的属性,而有些属性可能对分类任务没有太大作用,但是他们仍然可能会被选为最优属性。这种缺陷不是每次都会发生,只是存在一定的概率。解决这个问题可以选择信息增益比。

决策树的生成
- ID3算法:应用信息增益准则选择特征,递归地构建决策树
- C4.5算法:基于ID3算法进行改进,使用信息增益比来选择特征
决策树的剪枝
剪枝是决策树算法处理“过拟合”问题的主要手段。在决策树的学习中,为了尽可能的真确分类训练样本,不断递归的划分,优势造成决策树分支过多,对训练数据的分类很准确,但位置的数据分类没有那么准确,构建出的决策树过于复杂,产生过拟合。
剪枝是简化已生成的决策树的过程。具体地,从已生成的树上去掉一些子树或叶节点,将其根节点或父节点作为新的节点,简化树模型。