数组问题

1. 数字统计

题目描述

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。如果不存在则输出0。

解题思路

哈希法：先遍历一遍数组，利用Map存储每个元素出现的次数，在遍历一次Map，找出众数。

 
import java.util.HashMap;
import java.util.Set;
import java.util.Map;
public class Solution {
    public int MoreThanHalfNum_Solution(int [] array) {
        if(array.length==0){
            return 0;
        }
        int l = (int)(array.length / 2);
        Map<Integer, Integer> count = new HashMap<> ();
        for(int i=0; i<array.length; i++){
            int num = array[i];
            if(count.containsKey(num)){
                count.put(num, count.get(num)+1);
            }else{
                count.put(num, 1);
            }
        }
        Set<Integer> set = count.keySet();
        for(Integer k: set){
            Integer v = count.get(k);
            if(v.intValue() > l){
                return k.intValue();
            }
        }
        return 0;
    }
}
// 时间复杂度：O(n)
// 空间复杂度：O(n)

排序法：先将数组进行排序，众数一定在数组中间，再比遍历数组统计该数出现的次数，进行判断。

 
import java.util.Arrays;
public class Solution {
    public int MoreThanHalfNum_Solution(int [] array) {
        if(array.length==0){
            return 0;
        }
        Arrays.sort(array);
        int num = array[array.length / 2];
        int count = 0;
        for(int i=0; i<array.length; i++){
            if(array[i] == num){
                count ++;
            }
        }
        return count>(array.length / 2)?num:0;
    }
}           
// 时间复杂度：O(nlogn)
// 空间复杂度：O(1)

候选法（最优解):如果两个数不相等，就消去这两个数，最坏情况下，每次消去一个众数和一个非众数，那么如果存在众数，最后留下的数肯定是众数。

 
public class Solution {
    public int MoreThanHalfNum_Solution(int [] array) {
        int num = -1;
        int cnt = 0;
        for(int i=0; i<array.length; i++){
            if(cnt == 0){
                num = array[i];
                cnt ++;
            }else{
                if(num == array[i]){
                    cnt++;
                }else{
                    cnt --;
                }
            }
        }
        cnt = 0;
        for(int i=0; i<array.length; i++){
            if(array[i] == num){
                cnt ++;
            }
        }
        return cnt>(array.length/2)?num: 0;
    }
}
// 时间复杂度：O(n)
// 空间复杂度：O(1)

2. 连续子数组最大和

题目描述

HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢？例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组，返回它的最大连续子序列的和，你会不会被他忽悠住？(子向量的长度至少是1).

解题思路
这是一道典型的动态规划题目。最大子数组的和一定是由当前元素和之前最大连续子数组的和叠加在一起形成的。

假设dp[i]代表以当前元素a[i]为截止点的连续子序列的最大和;
若dp[i-1]>0, dp[i]=a[i]+dp[i-1], 因为当前数加上正数一定会变大;
若dp[i-1]<0, dp[i]=a[i], 因为当前数加上负数一定会变小；
使用max记录最大的dp值。 max=Math.max(max, dp[i]).

 
public class Solution {
    public int FindGreatestSumOfSubArray(int[] array) {
        int max = array[0];
        for(int i=1; i<array.length; i++){
            array[i] += array[i-1] > 0 ? array[i-1]: 0;
            max = Math.max(max, array[i]);
        }
        return max;
    }
}

3. 把数组排成最小的数

题目描述

输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。例如输入数组{3，32，321}，则打印出这三个数字能排成的最小数字为321323。

解题思路
将各个元素从小到大进行排序，排序之后再把他们串联起来。比较两个字符串s1, s2大小的时候，先将它们拼接起来，比较s1+s2,和s2+s1那个大，如果s1+s2大，那说明s2应该放前面，所以按这个规则，s2就应该排在s1前面。

 
import java.util.ArrayList;
public class Solution {
    public String PrintMinNumber(int [] numbers) {
        if(numbers.length == 0)
            return "";
        for(int i=0; i<numbers.length; i++){
            for(int j=i+1; j<numbers.length; j++){
                int s1 = Integer.parseInt(numbers[i] + "" + numbers[j]);
                int s2 = Integer.parseInt(numbers[j] + "" + numbers[i]);
                if(s1 > s2){
                    int temp = numbers[i];
                    numbers[i] = numbers[j];
                    numbers[j] = temp;
                }
            }
        }
        String str = new String("");
        for(int i=0; i<numbers.length; i++){
            str = str + numbers[i];
        }
        return str;
    }
}

4. 数组中的逆序对

问题描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。即输出P%1000000007

输入描述

题目保证输入的数组中没有的相同的数字
数据范围：
    对于%50的数据,size<=10^4
    对于%75的数据,size<=10^5
    对于%100的数据,size<=2*10^5

解题思路
归并排序法：
二路归并即merge，是将两个有序的序列合并为一个有序的序列，在两个子序列left、right合并过程中，当left中当前元素A小于right中当前元素B时，因为right序列已经有序，所以不用比较，A一定是left、right两个子序列当前剩余元素中最小的元素，这省去了A与B后其他元素比较的操作。

对于本题，在两个子序列left、right合并过程中，当left中当前元素A大于right中当前元素B时，因为left序列已经有序，所以不用比较，B一定小于left序列当前所有剩余元素，其全部可以与B组成逆序对，即通过一次比较可到一批逆序对，加速统计过程。

    
public class Solution {
    private int num = 0;
    public int InversePairs(int [] array) {
        if(array.length <= 1){
            return 0;
        }
        mergeSort(array, 0, array.length-1);
        return num; 
    }
    public void mergeSort(int[] array, int lo, int hi){
        if(lo >= hi){
            return;
        }
        int mid = lo + (hi - lo) / 2;
        mergeSort(array, lo, mid);
        mergeSort(array, mid+1, hi);
        merge(array, lo, mid, hi);
    }
    public void merge(int[] array, int lo, int mid, int hi){
        int i=lo, j=mid+1, k=0;
        int[] temp = new int[hi-lo+1];
        while(i<=mid && j<=hi){
            if(array[i]>array[j]){
                temp[k++] = array[j++];
                num += mid-i+1;
                num %= 1000000007;
            }else{
                temp[k++] = array[i++];
            }
        }
        while(i <= mid){
            temp[k++] = array[i++];
        }
        while(j <= hi){
            temp[k++] = array[j++];
        }
        for(int l=0; l<k; l++){
            array[lo+l] = temp[l];
        }
    }
}

数学问题

1. 统计1出现的次数

题目描述

求出1~13的整数中1出现的次数,并算出100~1300的整数中1出现的次数？为此他特别数了一下1~13中包含1的数字有1、10、11、12、13因此共出现6次,但是对于后面问题他就没辙了。ACMer希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中1出现的次数（从1 到 n 中1出现的次数）。

解题思路
https://leetcode-cn.com/problems/1nzheng-shu-zhong-1chu-xian-de-ci-shu-lcof/solution/mian-shi-ti-43-1n-zheng-shu-zhong-1-chu-xian-de-2/

https://www.nowcoder.com/questionTerminal/bd7f978302044eee894445e244c7eee6?answerType=1&f=discussion

2. 丑数

题目描述

把只包含质因子2、3和5的数称作丑数（Ugly Number）。例如6、8都是丑数，但14不是，因为它包含质因子7。习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。

解题思路
丑数能够分解成2^x3^y5^z, 所以只需要把得到的丑数不断地乘以2、3、5之后并放入他们应该放置的位置即可，而此题的难点就在于如何有序的放在合适的位置。
1乘以（2、3、5）=2、3、5；2乘以（2、3、5）=4、6、10；3乘以（2、3、5）=6,9,15；5乘以（2、3、5）=10、15、25；如果不加策略地添加丑数是会有重复并且无序，
而在2x，3y，5z中，如果x=y=z那么最小丑数一定是乘以2的，但关键是有可能存在x》y》z的情况，所以我们要维持三个指针来记录当前乘以2、乘以3、乘以5的最小值，然后当其被选为新的最小值后，要把相应的指针+1；因为这个指针会逐渐遍历整个数组，因此最终数组中的每一个值都会被乘以2、乘以3、乘以5，也就是实现了我们最开始的想法，只不过不是同时成乘以2、3、5，而是在需要的时候乘以2、3、5.

    
import java.util.ArrayList;
public class Solution {
    public int GetUglyNumber_Solution(int index) {
        if(index <= 0)
            return 0;
        int p2=0, p3=0, p5=0;
        int[] result = new int[index];
        result[0] = 1;
        for(int i=1; i<index; i++){
            result[i] = Math.min(result[p2]*2, Math.min(result[p3]*3, result[p5]*5));
            if(result[i] == result[p2]*2) p2++;
            if(result[i] == result[p3]*3) p3++;
            if(result[i] == result[p5]*5) p5++;
        }
        return result[index-1];
    }
}

3. 和为S的两个数字

题目描述

输入一个递增排序的数组和一个数字S，在数组中查找两个数，使得他们的和正好是S，如果有多对数字的和等于S，输出两个数的乘积最小的。

解题思路
双指针法:因为数组是有序的，所以可以用双指针，指向数组的首尾，具体步骤如下：

1.初始化：指针i指向数组首，指针j指向数组尾部;  
2. 如果arr[i] + arr[j] == sum , 说明是可能解;    
3. 否则如果arr[i] + arr[j] > sum, 说明和太大，所以--j;   
4. 否则如果arr[i] + arr[j] < sum, 说明和太小，所以++i.

    
import java.util.ArrayList;
public class Solution {
    public ArrayList<Integer> FindNumbersWithSum(int [] array,int sum) {
        ArrayList<Integer> ret  = new ArrayList<>();
        if(array.length<2){
            return ret;
        }
        int min = Integer.MAX_VALUE;
        int i=0;
        int j=array.length-1;
        while(i<j){
            int s = array[i] + array[j];
            if(s < sum){
                i++;
            }else if(s > sum){
                j--;
            }else{
                if(array[i]*array[j]<min){
                    ret.clear();
                    min=array[i]*array[j];
                    ret.add(array[i]);
                    ret.add(array[j]);   
                }
                i++;
            }
        }
        return ret;
    }
}

4. 和为S的连续正数序列

题目描述

输出所有和为S的连续正数序列。序列内按照从小至大的顺序，序列间按照开始数字从小到大的顺序。

解题思路

方法一：暴力法

求和为sum的连续子序列，可用暴力方法，算法步骤：
    1）用指针i枚举目标序列的左边界；
    2）用指针j枚举目标序列的右边界；
    3）用指针k枚举区间[i, j]，来计算区间和，看是否等于目标sum。

       
public class Solution { 
    public ArrayList<ArrayList<Integer> > FindContinuousSequence(int sum) {
       ArrayList<ArrayList<Integer>> ret = new ArrayList<>();
       for(int i=1; i<=sum/2; i++){
           for(int j=i+1; j<sum; j++){
               int tmp=0;
               for(int k=i; k<=j; k++){
                   tmp += k;
               }
               if(tmp == sum){
                   ArrayList<Integer> s = new ArrayList<>();
                   for(int k=i; k<=j; k++){
                       s.add(k);
                   }
                   ret.add(s);
               }else if(tmp > sum){
                   break;
               }
           }
       }
       return ret;
    }
}  
// 时间复杂度：O(N^3)
// 空间复杂度：O(1)

方法二：前缀和

对于求一个区间和，一贯的优化技巧是使用前缀和。比如：

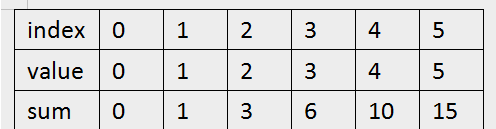
sum[i]表示前i个数的和。比如sum[1] = 1,表示前一个数的和为1，sum[2] = 3, 表示前2个数的和为3.
现在我们要求区间[2,4]表示求第2,3,4个数的和，就等于sum[4] - sum[1] = 9。 
代码中我们用一个变量来模拟这个前缀和。

     
public class Solution {  
    public ArrayList<ArrayList<Integer> > FindContinuousSequence(int sum) {
       ArrayList<ArrayList<Integer>> ret = new ArrayList<>();
        int temp=0;
        for(int i=1; i<=sum/2; i++){
           for(int j=i; j<sum; j++){
               temp += j;
               if(temp==sum){
                   ArrayList<Integer> s = new ArrayList<>();
                   for(int k=i; k<=j; k++){
                       s.add(k);
                   }
                   ret.add(s);
               }else if(temp > sum){
                   temp = 0;
                   break;
               }
           }
       }
       return ret;
    }
}  
// 时间复杂度：O(N^2)
// 空间复杂度：O(1)

方法三：滑动窗口

1. 什么是滑动窗口？
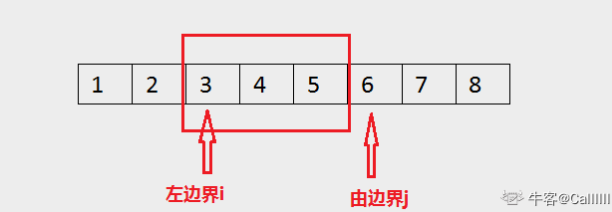
顾名思义，首先是一个窗口，既然是一个窗口，就需要用窗口的左边界i和右边界j来唯一表示一个窗口，
其次，滑动代表，窗口始终从左往右移动，这也表明左边界i和右边界j始终会往后移动，而不会往左移动。
这里我用左闭右开区间来表示一个窗口。比如：

2. 滑动窗口的操作
    * 扩大窗口，j += 1
    * 缩小窗口，i += 1
    算法步骤：
    1）初始化，i=1,j=1, 表示窗口大小为0
    2）如果窗口中值的和小于目标值sum， 表示需要扩大窗口，j += 1
    3）否则，如果狂口值和大于目标值sum，表示需要缩小窗口，i += 1
    4）否则，等于目标值，存结果，缩小窗口，继续进行步骤2,3,4

这里需要注意2个问题：
    *什么时候窗口终止呢，这里窗口左边界走到sum的一半即可终止，因为题目要求至少包含2个数
    *什么时候需要扩大窗口和缩小窗口？解释可看上述算法步骤。

  
public class Solution {
    public ArrayList<ArrayList<Integer> > FindContinuousSequence(int sum) {
        ArrayList<ArrayList<Integer>> ret = new ArrayList<>();
        int l=1;
        int r=1;
        int temp=0;
        while(l <= sum/2){
            if(temp < sum){
                temp += r;
                r++;
            }else if(temp > sum){
                temp -= l;
                l++;
            }else{
                ArrayList<Integer> s = new ArrayList<>();
                for(int k=l; k<r; k++){
                    s.add(k);
                }
                ret.add(s);
                temp -= l;
                l++;
            }
        }
       return ret;
    }
}       
// 时间复杂度：O(N)
// 空间复杂度：O(1)