“树”是数据结构中常见的非线性存储结构。在“树”结构中有一些常用的术语,总结为下:
- 父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点。
- 子节点:一个节点含有的子树的根节点称为该节点的子节点。
- 兄弟节点:拥有共同父节点的节点互称为兄弟节点。
- 度:节点的子树数目就是节点的度。
- 叶子节点:度为零的节点就是叶子节点。
- 节点的层次:从根节点开始,根节点为第一层,根的子节点为第二层,以此类推。
- 节点深度:对任意节点x,x节点的深度表示为根节点到x节点的路径长度。例如:根节点深度为0,第二层节点深度为1,以此类推。 “根节点—>节点的路径长度”
- 节点高度:对任意节点x,叶子节点到x节点的路径长度就是节点x的高度。 “节点—>叶子节点的路径长度”
- 树的深度:一棵树中节点的最大深度就是树的深度,也称为高度。
数据结构中有很多种树结构:二叉树,二叉搜索树, 红黑树,B+树等,下面对常见的几种树结构的的定义以及用途进行简单的介绍。
1. 二叉树
二叉树的定义:二叉树的每个结点最多只有二棵子树(不存在度大于2的结点)的树结构。每个节点有左右两个子节点。
二叉树示例:

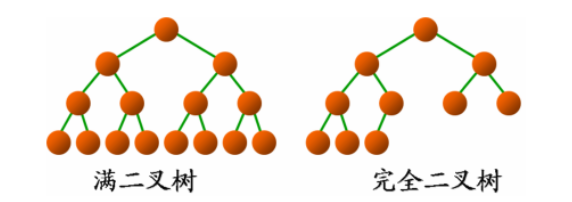
满二叉树 和 完全二叉树:
- 满二叉树:除最后一层无任何子节点外,每一层上的所有结点都有两个子结点。即除叶子结点外的所有结点均有两个子结点。节点数达到最大值,所有叶子结点都在同一层上。
完全二叉树:对于一颗二叉树,假设其深度为d(d>1)。除第d层外的所有节点构成满二叉树,且第d层所有节点从左向右连续地紧密排列,这样的二叉树被称为完全二叉树
示例:
判断一颗二叉树是否为完全二叉树
思路:利用层序遍历,如果我们当前遍历到了NULL结点,如果后续还有非NULL结点,说明是非完全二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public isBCT(TreeNode root){
if(root==null){
return true;
}
Queue<TreeNode> q = new Queue<TreeNode>();
boolean leaf = false;
q.push(root);
while(q!=null){
node = q.pop();
//如果已经碰到叶子结点,判断之后是否遇到非叶子节点
if((leaf&&(node.left!=null||node.right!=null))||(node.left==null&&node.right!=null)){
return false;
}
if(node.left!=null){
q.push(node.left);
}
if(node.right!=null){
q.push(node.right);
}
//判断是否为叶子节点
if((node.left!=null&&node.right==null)||(node.left==null&&node.right==null)){
leaf=true;
}
}
reurn true;
}
- 二叉树的性质:
- 在非空二叉树中,第i层的结点总数不超过2i-1, i>=1;
- 深度为d的二叉树最多有2d-1个结点(d>=1),最少有d个结点;
- 具有n个结点的完全二叉树的深度为log2(n+1);
2. 二叉查找树(二叉搜索树、二叉排序树、BST)
二叉查找树定义:二叉查找树又称二叉搜索树、二叉排序树、BST. 它是具有以下性质的二叉树:
- 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
- 左、右子树也分别为二叉排序树;
没有键值相等的节点。
示例左边的是BST,右边的不是:
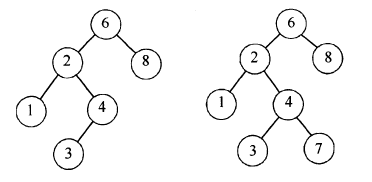
判断一颗二叉树是否为BST树
思路:根据二叉查找树的性质我们可以知道:如果我们用中序遍历遍历二叉查找树的话,遍历到的每个节点是依次增大的。根据这个思路,我们可以遍历一遍树,将遍历到的值保存到数组中,然后再判断这个数组是否为递增数组就可以了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20//递归实现
int last = Integer.MIN_VALUE;
public isBST(TreeNode root){
if(root==null){
return true;
}
if(!isBST(root.left)){
return false;
}
if(root.val <= last){
return false;
}
last = root.val;
if(!isBST(root.right)){
return false;
}
return true;
}
//非递归实现
对二叉查找树进行中序遍历,即可得到有序的数列。
- 它和二分查找一样,插入和查找的时间复杂度均为O(logn),但是在最坏的情况下仍然会有O(n)的时间复杂度。
- 二叉查找树的高度决定了二叉查找树的查找效率。
3. 二叉树的操作
二叉树的遍历
二叉树有三种遍历方式:
- 先序遍历:先访问根节点,再前序遍历左子树,最后前序遍历右子树。
- 中序遍历:先中序访问左子树,再访问根节点,再中序访问右子树。中序遍历得到一个有序(递增)的数列。
- 后序遍历:先后序访问左子树,再后序访问右子树,再访问根节点。
递归实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// 二叉树的定义
public class TreeNode{
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val){
this.val = val;
}
}
// 先序遍历 (根节点->左子树->右子树)
public void PreOrderTraversal(TreeNode root){
System.out.println(root.val);
PreOrderTraversal(root.left);
PreOrderTraversal(root.right);
}
// 中序遍历 (左子树->根节点->右子树)
public void InOrderTraversal(TreeNode root){
InOrderTraversal(root.left);
System.out.println(root.val);
InOrderTraversal(root.right);
}
// 后序遍历 (左子树->右子树->根节点)
public void PostOrderTraversal(TreeNode root){
PostOrderTraversal(root.left);
PostOrderTraversal(root.right);
System.out.println(root.val);
}非递归实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
// 二叉树的定义
public class TreeNode{
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val){
this.val = val;
}
}
// 先序遍历 (根节点->左子树->右子树)
public void PreOrderTraversal(TreeNode root){
LinkedList<TreeNode> stack = new LinkedList<TreeNode>();
while(!stack.isEmpty() || root!=null){
if(root!=null){
System.out.println(root.val);
stack.push(root);
root = root.left;
}else{
root = root.pop();
root = root.right;
}
}
}
// 中序遍历 (左子树->根节点->右子树)
public void InOrderTraversal(TreeNode root){
LinkedList<TreeNode> stack = new LinkedList<TreeNode>();
while(!stack.isEmpty() || root!=null){
if(root!=null){
stack.push(root);
root = root.left;
}else{
root = root.pop();
System.out.println(root.val);
root = root.right;
}
}
}
// 后序遍历 (左子树->右子树->根节点)
public void PostOrderTraversal(TreeNode root){
LinkedList<TreeNode> stack = new LinkedList<>();
HashMap<Integer, Integer> map = new HashMap<>();
TreeNode tmp;
while(!stack.isEmpty() || root!=null){
if(root!=null){
stack.push(root.val);
map.put(root.val, 1);
root = root.left;
}else{
tmp=stack.getFirst();
if(map.get(tmp.val)==2){
stack.pop();
System.out.println(tmp.val);
root=null;
}else{
map.put(tmp.val, 2);
root = tmp.right;
}
}
}
}参考博客:
https://www.cnblogs.com/bigsai/p/11393609.html
https://www.cnblogs.com/hapjin/p/5679482.html二叉树的层级遍历
二叉树的层级遍历需要借助一个队列(queue)来保存当前节点的子节点。 1. 初始化:一个队列queue,将root节点入队列q 2. 如果队列不空,做如下操作: 3. 弹出队列头,保存为node,将node的左右非空孩子加入队列 4. 重复2,3步骤,直到队列为空 以上图左子图为例: 1. 创建空队列q=[]; 2. 将根节点6入队列,q=[6]; 3. 队列不空,取出队列中头元素6,若6节点左右子节点不空,入队,q=[2,8]; 4. 队列不空,取出头元素2,将节点2的左右子节点入队,q=[8,1,4]; 5. 重复上述步骤,直到队列为空。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import java.util.Queue;
import java.util.LinkedList;
import java.util.ArrayList;
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
public int TreeDepth(TreeNode root) {
if(root == null){
return 0;
}
ArrayList<TreeNode> ret = new ArrayList<>();
Queue<TreeNode> q = new LinkedList<TreeNode>();
q.add(root);
while(q.size()!=0){
TreeNode node = q.poll();
ret.add(node);
if(node.left != null){
q.add(node.left);
}
if(node.right != null){
q.add(node.right);
}
}
}若需记录树的深度或有几层,可作如下改进:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
//递归方法
public class Solution {
public int TreeDepth(TreeNode root) {
if(root == null)return 0;
int ld = TreeDepth(root.left);
int rd = TreeDepth(root.right);
return Math.max(ld,rd) + 1;
}
}
//非递归方法
public class Solution {
public int TreeDepth(TreeNode root) {
if(root == null){
return 0;
}
Queue<TreeNode> q = new LinkedList<TreeNode>();
q.add(root);
int level = 0;
int size;
TreeNode node;
while(q.size()!=0){
size = q.size();
while(size != 0){
node = q.poll();
if(node.left != null){
q.add(node.left);
}
if(node.right != null){
q.add(node.right);
}
size--;
}
level++;
}
return level;
}
}二叉查找树插入节点操作
二叉查找树的插入过程如下:
1) 若当前的二叉查找树为空,则插入的元素为根节点;
2) 若插入的元素值小于根节点值,则将元素插入到左子树中;
3) 若插入的元素值不小于根节点值,则将元素插入到右子树中。
二叉查找树删除节点操作
二叉查找树的删除,分三种情况进行处理:
1)p为叶子节点,直接删除该节点,再修改其父节点的指针(注意分是根节点和不是根节点),如图a;
2)p为单支节点(即只有左子树或右子树)。让p的子树与p的父亲节点相连,删除p即可(注意分是根节点和不是根节点),如图b;
3)p的左子树和右子树均不空。找到p的后继y,y为这个节点右子树的最小值或者左子树的最大值。 如图c。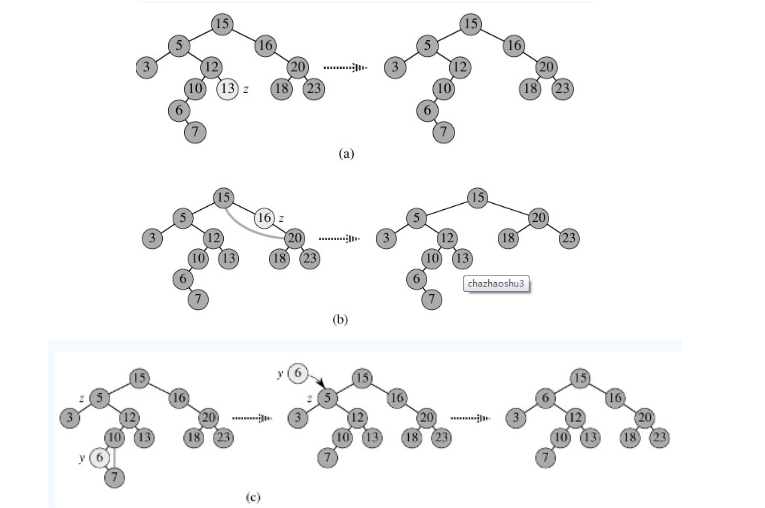
4. 平衡二叉树
对于一般的二叉搜索树,其期望高度(即为一棵平衡树时)为log2n,其各操作的时间复杂度O(log2n)同时也由此而决定。但是,在某些极端的情况下(如在插入的序列是有序的时),二叉搜索树将退化成近似链或链,此时,其操作的时间复杂度将退化成线性的,即O(n)。我们可以通过随机化建立二叉搜索树来尽量的避免这种情况,但是在进行了多次的操作之后,由于在删除时,我们总是选择将待删除节点的后继代替它本身,这样就会造成总是右边的节点数目减少,以至于树向左偏沉。这同时也会造成树的平衡性受到破坏,提高它的操作的时间复杂度。于是就有了我们下边介绍的平衡二叉树。
平衡二叉树(Balanced Binary Tree):又被称为AVL树(有别于AVL算法),且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。 并且平衡二叉树必定是二叉搜索树。平衡二叉树的常用算法有红黑树、AVL树等。在平衡二叉搜索树中,我们可以看到,其高度一般都良好地维持在O(log2n),大大降低了操作的时间复杂度。
最小二叉平衡树的节点的公式为:F(n)=F(n-1)+F(n-2)+1
这个类似于一个递归的数列,可以参考Fibonacci数列,1是根节点,F(n-1)是左子树的节点数量,F(n-2)是右子树的节点数量。
判断一颗二叉树是不是平衡二插树1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public class Solution {
public boolean IsBalanced_Solution(TreeNode root) {
return depth(root) != -1;
}
public int depth(TreeNode root){
if(root == null)return 0;
int left = depth(root.left);
if(left == -1)return -1; //如果发现子树不平衡之后就没有必要进行下面的高度的求解了
int right = depth(root.right);
if(right == -1)return -1;//如果发现子树不平衡之后就没有必要进行下面的高度的求解了
if(left - right <(-1) || left - right > 1)
return -1;
else
return 1+(left > right?left:right);
}
}
AVL树的查找、插入和删除在平均和最坏情况下都是O(logn)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。这个方案很好的解决了二叉查找树退化成链表的问题,把插入,查找,删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间,不过相对二叉查找树来说,时间上稳定了很多。
AVL树平衡操作:
https://blog.csdn.net/qq_25343557/article/details/89110319
https://www.cnblogs.com/zhuwbox/p/3636783.html
5. 红黑树
红黑树的定义:红黑树是一种自平衡二叉查找树。它是复杂的,但它的操作有着良好的最坏情况运行时间,并且在实践中是高效的: 它可以在O(logn)时间内做查找,插入和删除,这里的n是树中元素的数目。
红黑树和AVL树一样都对插入时间、删除时间和查找时间提供了最好可能的最坏情况担保。
红黑树与AVL树的区别:
区别:
1)红黑树放弃了追求完全平衡,追求大致平衡,在与平衡二叉树的时间复杂度相差不大的情况下,保证每次插入最多只需要三次旋转就能达到平衡,实现起来也更为简单。
2)平衡二叉树追求绝对平衡,条件比较苛刻,实现起来比较麻烦,每次插入新节点之后需要旋转的次数不能预知。
共同点:
进行插入或者删除是都是需要进行一定的平衡操作的。
红黑树的性质:
红黑树是每个节点都带有颜色属性的二叉查找树,颜色为红色或黑色。在二叉查找树强制的一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
性质1. 节点是红色或黑色。
性质2. 根是黑色。
性质3. 所有叶子都是黑色(叶子是NIL节点)。
性质4. 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
性质5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
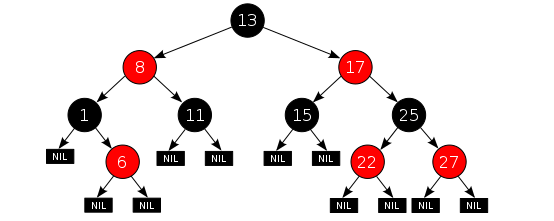
参考:
书籍《算法 第四版》
https://www.cnblogs.com/maybe2030/p/4732377.html
https://blog.csdn.net/u014532217/article/details/79118023
https://blog.csdn.net/qq_31709249/article/details/103092783
常见的二叉树算法题
1. 二叉树中和为某一值的路径
题目描述:
输入一颗二叉树的根节点和一个整数,按字典序打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
1 |
|
2. 路径总和(Leetcode 112)
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
方法一:递归法
1 |
|
方法二:广度优先搜索
1 | public boolean hasPathSum(TreeNode root, int sum) { |
3. 求根到叶子节点数字之和(LeetCode 129)
给定一个二叉树,它的每个结点都存放一个 0-9 的数字,每条从根到叶子节点的路径都代表一个数字。
例如,从根到叶子节点路径 1->2->3 代表数字 123。
计算从根到叶子节点生成的所有数字之和。
说明: 叶子节点是指没有子节点的节点。
示例 1:
输入: [1,2,3]
1
/ \
2 3
输出: 25
解释:
从根到叶子节点路径 1->2 代表数字 12.
从根到叶子节点路径 1->3 代表数字 13.
因此,数字总和 = 12 + 13 = 25.
方法一:递归法
1 | class Solution { |
方法二:广度优先搜索
1 | class Solution { |
4. 二叉树的所有路径(LeetCode 257)
给定一个二叉树,返回所有从根节点到叶子节点的路径
示例:
输入:
1
/ \
2 3
\
5
输出: ["1->2->5", "1->3"]
1 | class Solution { |
5.
6. 路径总和 III(LeetCode 437)
给定一个二叉树,它的每个结点都存放着一个整数值。
找出路径和等于给定数值的路径总数。
路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
二叉树不超过1000个节点,且节点数值范围是 [-1000000,1000000] 的整数。
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8
10
/ \
5 -3
/ \ \
3 2 11
/ \ \
3 -2 1
返回 3。和等于 8 的路径有:
1. 5 -> 3
2. 5 -> 2 -> 1
3. -3 -> 11
方法一:递归法
1 |
|
2. 二叉搜索树的后序遍历序列
题目描述:
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回true,否则返回false。假设输入的数组的任意两个数字都互不相同。
1 |
|