堆的定义
堆这种数据结构是一种完全二叉树,堆分为最大堆和最小堆
- 最大堆:二叉树中的任一顶点大于等于它的左右子节点
- 最小堆:二叉树中的任一顶点小于等于它的左右子节点
堆可以用数组来存储表示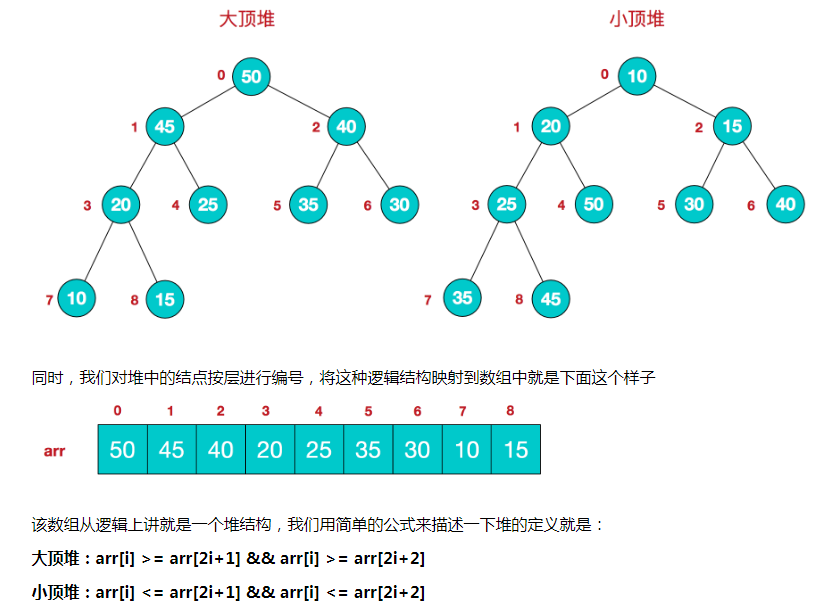
优先队列
优先队列(Priority Queue):特殊的队列,取出元素的顺序按照元素的优先权或关键字的大小,不是元素入队的先后顺序。
优先队列(堆)的使用场景:
1. 任何时候返回最值元素;
2. 数据太大存不下,要找出一定的最值元素;
3. 合并若干不同来源的已经排序的源(索引优先队列)
优先队列的实现方式:
基于堆的优先队列
用堆实现优先队列的方法:
注:以下代码存储数据时从数组的下标1开始
代码实现:
最大堆实现的最大优先队列1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
public class MaxPQ<T extends Comparable<T>>{
private T[] pq; //存队列数据的数组
private int N=0; //最终元素的个数
//构造函数
public MaxPQ(int maxN){
pq=(T[])new Comparable[maxN+1];
}
//判断队列是否为空
public boolean isEmpty(){
return N==0;
}
//返回队列元素个数
public int size(){
return N;
}
//插入数据
public void insert(T v){
pq[++N]=v;
swim(N);
}
//删除队列中最大元素并返回最大值
public T delMax(){
T max=pq[1];
exch(1,N--);
pq[N+1]=null;
sink(1);
return max;
}
//上浮
private void swim(int k){
while(k>1 && less(k/2,k)){
exch(k/2,k);
k=k/2;
}
}
//下沉
private void sink(int k){
while(2*k<=N){
int t=2*k;
if(t<N && less(t,t+1)){
t++;
}
if(less(k,t)){
exch(k,t);
}else{
break;
}
k=t;
}
}
private boolean less(int i,int j){
return pq[i].compareTo(pq[j])<0;
}
private void exch(int i,int j){
T temp=pq[i];
pq[i]=pq[j];
pq[j]=temp;
}
public static void main(String[] args){
MaxPQ<Integer> p=new MaxPQ<Integer>(10);
int n=5;
p.insert(88);
p.insert(2);
p.insert(56);
p.insert(3);
p.insert(42);
while(n>0){
System.out.println(p.delMax());
n--;
}
}
}
代码实现的最主要的功能是实现元素的优先级,快速找到并删除最大元素,插入元素(自动调整)
算法分析:
- 一颗大小为N的完全二叉树的高度为lgN;
- 含有N个元素的基于堆的优先队列,插入元素需要不超过lgN+1次比较,删除最大元素需要不超过2lgN次比较;
最小堆实现的最小优先队列1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51public class MinPQ<T extends Comparable<T>> {
private T[] pq;
private int N;
public MinPQ(int maxN){
pq=(T[])new Comparable[maxN+1];
}
public boolean isEmpty(){
return N==0;
}
public int size(){
return N;
}
public void insert(T v){
pq[++N]=v;
swim(N);
}
private void swim(int k){
while(k>1 && less(k,k/2)){
exch(k,k/2);
k=k/2;
}
}
public T deleteMin(){
T min=pq[1];
exch(1,N--);
sink(1);
return min;
}
private void sink(int k){
while(2*k<N){
int t=2*k;
if(t<k && less(t+1,t)){
t++;
}
if(less(t,k)){
exch(t,k);
}else{
break;
}
k=t;
}
}
private boolean less(int v,int w){
return pq[v].compareTo(pq[w])<0;
}
private void exch(int v,int w){
T temp=pq[v];
pq[v]=pq[w];
pq[w]=temp;
}
}索引优先队列
优先队列的一个缺点是无法直接访问队列中的元素(除了直接找到最大或最小的元素),对其更新修改。
用过建立索引优先队列来实现快速索引。创建两个数组:elements[]用来存储队列中的对象(不需要按连续存储),pq[]用来存储队列中每个对象在elements[]中的索引。 通过这两个数组建立的映射关系,在构建优先队列的时候,不需要变动elements[],只需要维护改变pq中的元素即可。当向队列中插入一个新的对象时,在elements中存储该对象,将其索引存储在pq中,并对这个索引值进行上浮操作维护优先队列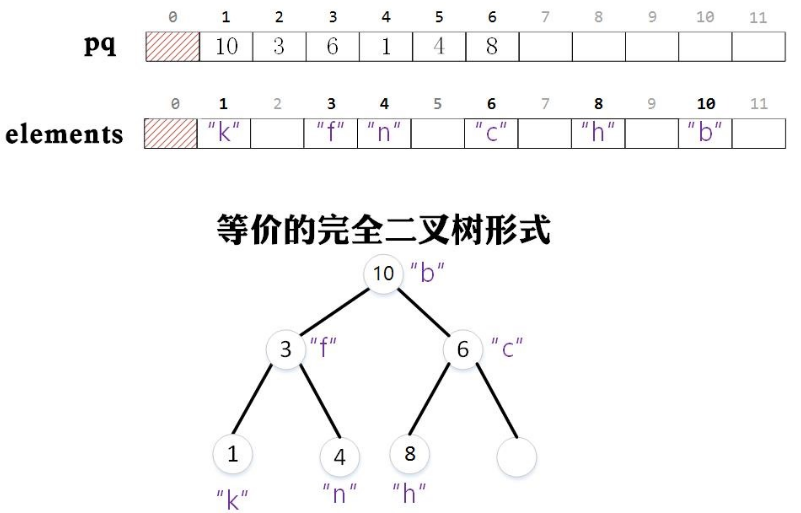
在操作队列时,如果想更改队列中某个对象,比如像将索引为3的位置改为”b”,那么直接操作elements[3]=”b”,这时需要重新调整维护优先队列,在pq数组中队值为3的元素操作,但是并不知道pq中那个位置的值是3,只能通过顺序遍历查找。为了方便查找pq中的元素,创建一个qp数组,将pq中元素作为索引在qp中存储该元素在pq中的索引。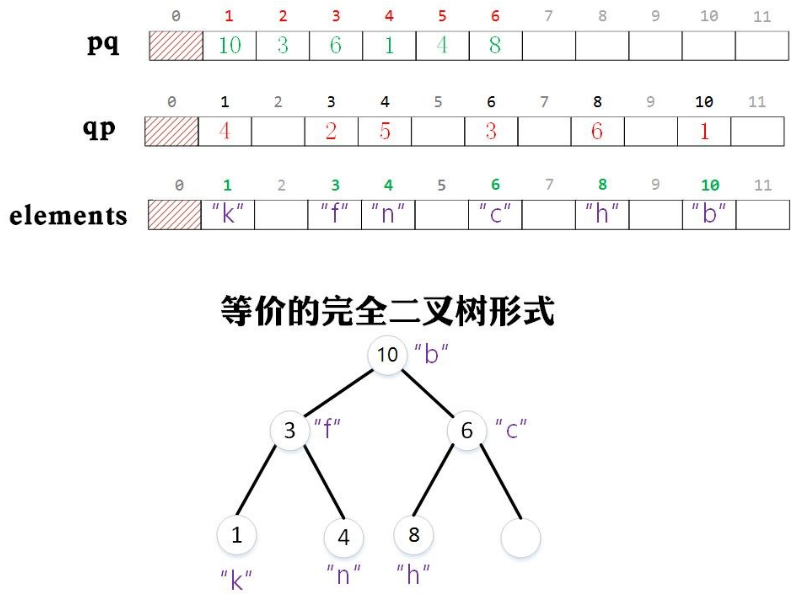
在队列的操作中经常要交换两个元素,交换pq中的两个元素的同事也要交换qp中相应位置的元素。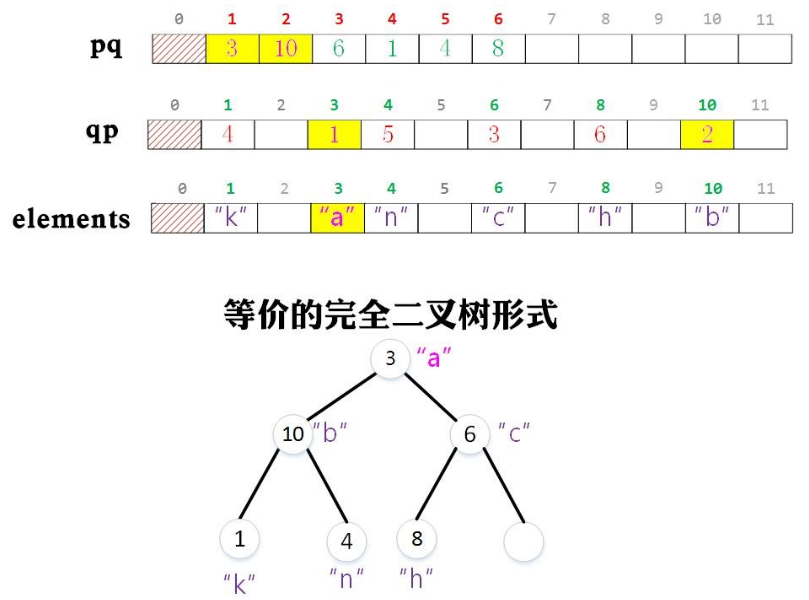
索引最小优先队列1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103public class IndexMinPQ<Key extends Comparable<Key>> {
private int pq[];
private int qp[];
private Key keys[];
private int maxN;
private int N;
public IndexMinPQ(int maxN){
this.maxN=maxN;
N=0;
pq=new int[maxN+1];//这些数组中0索引处不存储值
qp=new int[maxN+1];
keys=(Key[])new Comparable[maxN];
for(int i=0;i<=maxN;i++){
qp[i]=-1;
}
}
public boolean isEmpty(){
return N==0;
}
public int size(){
return N;
}
public boolean contains(int i){
//这里的i检查的是keys在索引i处是否有值
if(i<0 || i>maxN){
throw new IllegalArgumentException();
}
return qp[i]!=-1;
}
public void insert(int k,Key key){
if ( k< 0 || k> maxN) throw new IllegalArgumentException();
if (contains(k)) throw new IllegalArgumentException("index is already in the priority queue");
keys[k]=key;
pq[++N]=k;
qp[k]=N;
swim(N);
}
//返回队列中的最小值
public Key minKey(){
return keys[pq[1]];
}
//删除并返回队列中的最小值
public Key deleteMin(){
if (N == 0) throw new NoSuchElementException("Priority queue underflow");
Key min=keys[pq[1]];
pq[1]=pq[N--];
sink(1);
return min;
}
//删除并返回队列中的某个值
public void delete(int k){
if (k < 0 || k > maxN) throw new IllegalArgumentException();
if (!contains(k)) throw new NoSuchElementException("index is not in the priority queue");
int index=qp[k];
pq[index]=pq[N--];
swim(index);
sink(index);
keys[k]=null;
qp[k]=-1;
}
//改变队列中某个对象的值
public void changeKey(int k,Key key){
if (k < 0 || k > maxN) throw new IllegalArgumentException();
if (!contains(k)) throw new NoSuchElementException("index is not in the priority queue");
keys[k]=key;
swim(qp[k]);
sink(qp[k]);
}
//上浮调整
private void swim(int k){
while(k>1){
if(less(k,k/2)){
exch(k,k/2);
}
k=k/2;
}
}
//下沉调整
private void sink(int k){
while(2*k<=N){
int t=2*k;
if(t<N && less(t+1,t)){
t=t+1;
}
if(less(k,t)){
exch(k,t);
}else{
break;
}
k=t;
}
}
private boolean less(int k,int v){
return keys[pq[k]].compareTo(keys[pq[v]])<0;
}
private void exch(int k,int v){
int temp=pq[k];
pq[k]=pq[v];
pq[v]=temp;
qp[pq[k]]=k;
qp[pq[v]]=v;
}
}
堆排序
堆排序分为两个阶段,给定一个无序的数组,首先要做的事构造堆。
a.将无需序列构建成一个堆,根据升序降序需求选择最大堆或最小堆;
b.将堆顶元素与末尾元素交换,将最大元素”沉”到数组末端,N–将最大的元素固定,再次调整不在去管它;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
对于给定的无序构造堆的一个高效方法就是从右向左进行sink下沉操作,不需要管叶子结点(叶子结点已经算作一个有堆,无法进行下沉操作),所以只需要扫描一半的数组元素。
示意图: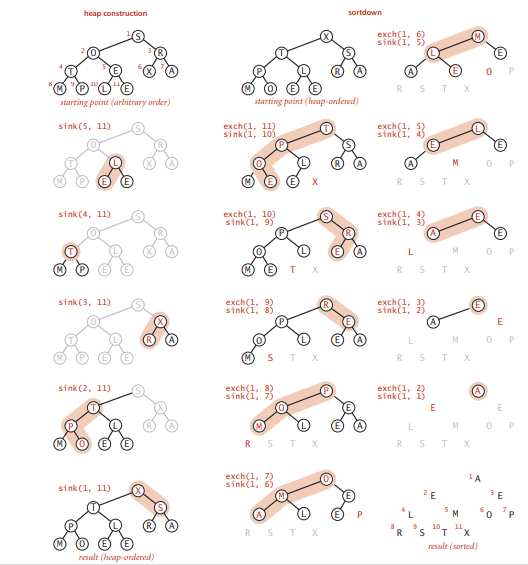
堆排序算法实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
public class HeapSort<T extends Comparable<T>> extends Sort<T> {
public void sort(T[] a){
//数组a[0]不存储哨兵,a[0]的值一般用作,从a[1]开始
int N=a.length-1;
//构建堆
for(int k=N/2;k>=1;k--){
sink(a,k,N);
}
//堆排序
while(N>1){
exch(a,1,N--);
sink(a,1,N);
}
}
private void sink(T[] a,int k,int N){
while(2*k<=N){
int j=2*k;
if(j<N && less(a[j],a[j+1])){
j++;
}
if(less(a[k],a[j])){
exch(a,k,j);
}else{
break;
}
k=j;
}
}
public static void main(String[] args){
HeapSort<String> b=new HeapSort<String>();
String[] str={"q","sss","aaa","ccc","qqq","bbb"};
b.sort(str);
for(int i=1;i<=str.length-1;i++){
System.out.println(str[i]);
}
}
}
算法分析:
- 用下沉法构建堆(N个元素)只需少于2N次比较和少于N次的交换;
- 对N个元素的堆排序,需要少于(2NlgN+2N)次比较,一半次数的交换;
多种算法比较
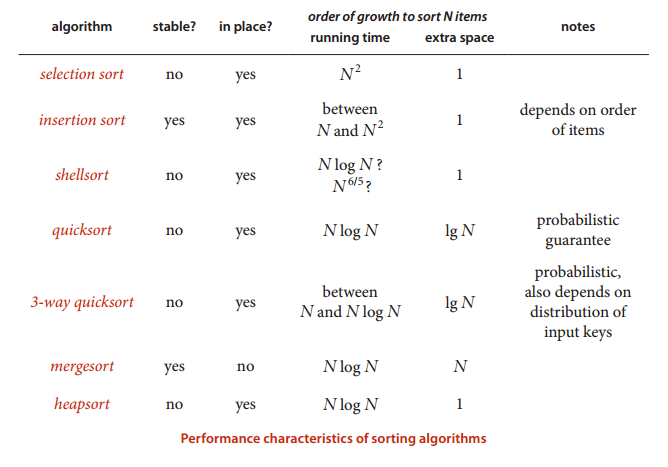
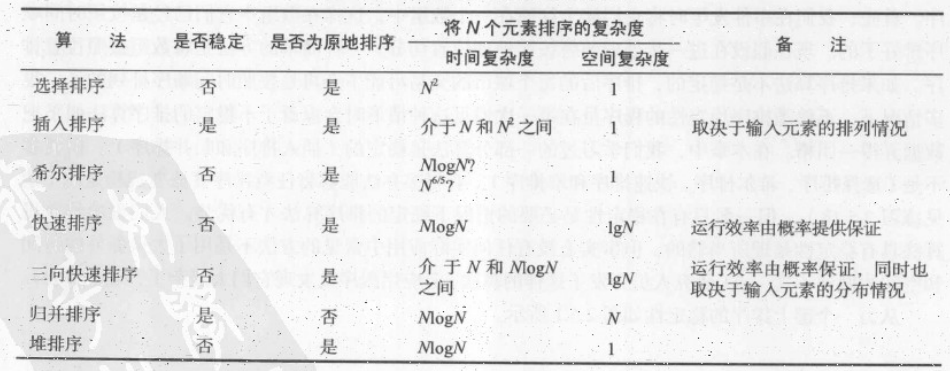
快速排序是最快的通用排序方法
因为快速排序内循环指令少,他还能利用缓存(因为总是顺序访问数组),时间复杂度都是~cNlgN,使用三向切分后可能将某些时间复杂度变为线性级的。
Java 主要排序方法为 java.util.Arrays.sort(),对于原始数据类型使用三向切分的快速排序,对于引用类型使用归并排序